Question

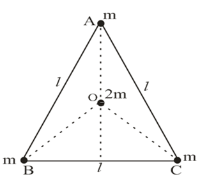
An equilateral triangle $ABC$ of side $l$ having three point masses $m$ at the three vertices is shown in figure. Calculate the force acting on a mass $2m$ , if it is placed at the centroid $O$ of the triangle.

• A. zero
• B. $\frac{3 G m^{2}}{l^{2}}$
• C. $\frac{5 G m^{2}}{l^{2}}$
• D. $\frac{7 G m^{2}}{l^{2}}$

Answer 1

Answer: (A)

Draw a perpendicular $AD$ to the side $BC$ .
$AD=ABsin 60^{o}=\frac{\sqrt{2}}{3}l$
Distance $AO$ of the centroid $O$ from $A$ is $\frac{2}{3}$ $AD$ .
$ \, AO=\frac{2}{3}\left(\frac{\sqrt{3}}{2} l\right)=\frac{l}{\sqrt{3}}$
By symmetry, $AO=BO=CO=\frac{1}{\sqrt{3}}$
Force on mass $2m$ at $O$ due to mass m at A is
$F_{O A}=\frac{G m \left(\right. 2 m \left.\right)}{\left(\right. l / \sqrt{3} \left.\right)^{2}}=\frac{6 G m^{2}}{l^{2}} \, along \, OA$
Force on mass $2m$ at $O$ due to mass m at $B$ is
$F_{O B}=\frac{G m \left(\right. 2 m \left.\right)}{\left(\right. l / \sqrt{3} \left.\right)^{2}}=\frac{6 G m^{2}}{l^{2}}along \, OA$
Force on mass $2m$ at $O$ due to mass $m$ at $C$ is
$F_{O C}=\frac{G m \left(\right. 2 m \left.\right)}{\left(\right. l / \sqrt{3} \left.\right)^{2}}=\frac{6 G m^{2}}{l^{2}} \, along \, OC$
Draw a line PQ parallel to BC passing through O. Then $\angle BOP=30º=\angle COQ$
Resolving $\overset{ \rightarrow }{F}_{O B}$ and $\overset{ \rightarrow }{F}_{O C}$ into two components.
Components acting along $OP$ and $OQ$ are equal in magnitude and opposite in direction. So, they will cancel out while the components acting along $OD$ will add up.
$ \, \therefore $ he resultant force on the mass $2m$ at $O$ is
$F_{R}=F_{O A}-\left(\right.F_{O B}sin30º+F_{O C}sin30º\left.\right)$ .
$=\frac{6 G m^{2}}{l^{2}}-\left(\right.\frac{6 G m^{2}}{l^{2}}\times \frac{1}{2}+\frac{6 G m^{2}}{l^{2}}\times \frac{1}{2}\left.\right)=0$