Q.
An equilateral triangle $ABC$ is cut from a thin solid sheet of wood. (see figure) $D, E$ and $F$ are the mid-points of its sides as shown and $G$ is the centre of the triangle. The moment of inertia of the triangle about an axis passing through and perpendicular to the plane of the triangle is $I_0$. It the smaller triangle $DEF$ is removed from $ABC$, the moment of inertia of the remaining figure about the same axis is $I$. Then: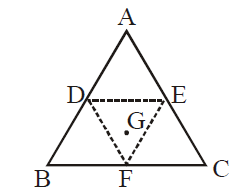
Solution: