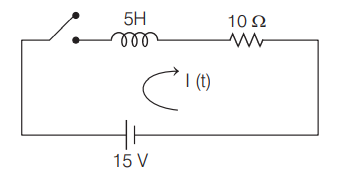
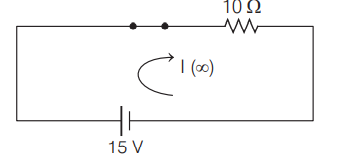
Question

An emf of $15\, V$ is applied to a circuit containing $5\, H$ inductance and $10\, \Omega$ resistance. The ratio of currents at time $t = \infty$ and $t = 1\, s$ is

• A. $\frac{e}{e^2 -1}$
• B. $\frac{e^2}{e -1}$
• C. $\frac{e}{1 - e^2 }$
• D. $\frac{e^2 }{e^2 -1}$

Answer 1

Answer: (D)

According to the question, The circuit as shown below,

The current in the circuit,
$I(t) = I(\infty) - [I(\infty) - I(0)]e^{-t/\tau} \dots$(i)
$\because$ Time constant, $\tau = \frac{L}{R} = \frac{5}{10} = \frac{1}{2} sec$
at $t \to \infty$, inductor behaves as short circuit hence circuit will be

So, $I(\infty)=\frac{15}{10}=1.5 \,A \dots$(ii)
at $t \rightarrow 0$, inductor behaves as open circuit
so, no current flow in the circuit, $I(0)=0$
So from Eq. (i),
$\Rightarrow I(t) =1.5-(1.5-0) e^{\frac{-t}{(1 / 2)}}=1.5\left(1-e^{-2 t}\right) $
at $ t =1 \,sec , \Rightarrow I(1)=1.5\left(1-e^{-2}\right) \ldots$ (iii)
From Eq. (ii) and (iii), we get
$\Rightarrow \frac{I(\infty)}{I(1)}=\frac{1.5}{1.5\left(1-e^{-2}\right)}=\frac{e^{2}}{e^{2}-1}$