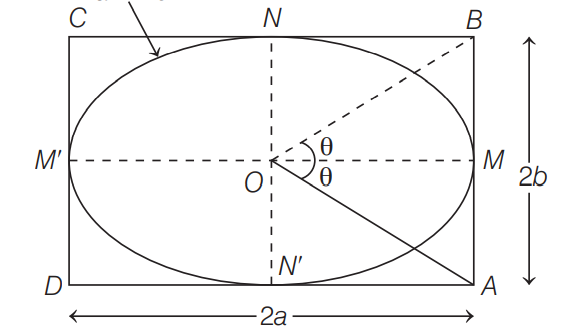
Question

An ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b)$ is inscribed in a rectangle of dimensions $2 a$ and $2 b$ respectively, If the angle between the diagonals of the rectangle is $\tan ^{-1}(4 \sqrt{3})$, then the eccentricity of that ellipse is

• A. $\frac{1}{\sqrt{2}}$
• B. $\frac{1}{2}$
• C. $\frac{1}{\sqrt{3}}$
• D. $\frac{\sqrt{2}}{\sqrt{3}}$

Answer 1

Answer: (B)

Now, from the figure $\tan \theta=\frac{b}{a}$
$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$

Since, $\tan 2 \theta=\frac{2 \tan \theta}{1-\tan ^{2} \theta}$
[where $2 \theta$ is angle between the diagonals of the rectangle ]
$\Rightarrow 4 \sqrt{3}=\frac{2 \frac{b}{a}}{1-\frac{b^{2}}{a^{2}}} $
$\Rightarrow 2 \sqrt{3}=\frac{\frac{b}{a}}{1-\frac{b^{2}}{a^{2}}}\left[\because \tan ^{-1}(4 \sqrt{3})=2 \theta\right]$
$\Rightarrow 2 \sqrt{3}\left(\frac{b}{a}\right)^{2}+\left(\frac{b}{a}\right)-2 \sqrt{3}=0$
$\Rightarrow 2 \sqrt{3}\left(\frac{b}{a}\right)^{2}+4\left(\frac{b}{a}\right)-3\left(\frac{b}{a}\right)-2 \sqrt{3}=0$
$\Rightarrow 2\left(\frac{b}{a}\right)\left[\sqrt{3}\left(\frac{b}{a}\right)+2\right]-\sqrt{3}\left[\sqrt{3}\left(\frac{b}{a}\right)+2\right]=0$
$\Rightarrow \left[2\left(\frac{b}{a}\right)-\sqrt{3}\right]\left[\sqrt{3}\left(\frac{b}{a}\right)+2\right]=0$
$\Rightarrow \frac{b}{a}=\frac{\sqrt{3}}{2} \,\,\,\left\{\text { as } \frac{b}{a}>0\right\}$
Now, the eccentricity of the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ is
$e=\sqrt{1-\left(\frac{b}{a}\right)^{2}}=\sqrt{1-\frac{3}{4}}=\sqrt{\frac{1}{4}}=\frac{1}{2}$