Question

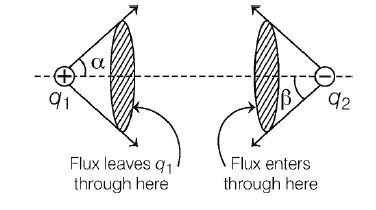
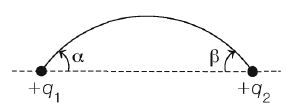
An electrostatic field line leaves at an angle $\alpha$ from point charge $q_{1}$ and connects with point charge $- q_{2}$ a tan angle $\beta$($q_{1}$ and $q_{2}$ are positive) see figure below. If $q_{2}=\frac{3}{2}q_{1}$ and $\alpha=30^{\circ},$ then

• A. $0°\:<\:\beta \:<\:30°$
• B. $\:\beta =30^{\circ }\:$
• C. $30^{\circ }<\beta \le 60^{\circ }$
• D. $60^{\circ }<\beta \le 90^{\circ }$

Answer 1

Answer: (A)

Consider another symmetric field line below line joining centres of charges $q_1$ and $q_2$

In given situation, flux (field lines) leaving charge $q_1$ at a solid angle
$2\alpha =$ flux terminating over charge $q_2$ at a solid angle$2\beta$.
Clearly, in given situation

We can say that, flux leaving charge $q^1$ through a cone of semi-vertical angle $\alpha =$ flux terminating on charge $q_2$ through a cone of semi-vertical angle $\beta$..

To calculate flux, we first find flux through an elemental ring of base of cone and then we integrate to get total flux.

Area of elemental ring,
$dA = 2\pi r ds = 2\pi R \sin\alpha• Rd \alpha$
Flux through elemental ring $(E||dA)$
$d\phi=\frac{kQ}{R^{2}}\cdot2\pi R^{2}\sin \alpha d\alpha$
Total flux through base of cone
$\phi=\int\limits_{o}^{\alpha}\frac{kQ}{R^{2}}\cdot2\pi R^{2} \sin \alpha d\alpha$
$ =kQ2\pi\int\limits_{o}^{\alpha} \sin \alpha d\alpha$
$\phi=\frac{Q}{2\varepsilon_{o}}.\left(1-cos\alpha\right)$
So, equating flux of both cones, we get
$\frac{q_{1}}{2\varepsilon_{o}}\left(1-\cos\alpha\right)=\frac{q_{2}}{2\varepsilon_{o}}\left(1-\cos\beta\right) K$
$\Rightarrow q_{1}\left(1-\cos\alpha\right)=\frac{3}{2}q_{1}\left(1-\cos\beta\right)$
Substituting $\alpha = 30°$ in above equation, we get
$\Rightarrow \frac{2}{3}\left(1-\cos 30^{\circ}\right)=1-\cos \beta$
$\Rightarrow \frac{2}{3}\left(1-\sqrt{\frac{3}{2}}\right)=1-\cos\beta$
$\cos\beta=1-\frac{2}{3}\left(1-\sqrt{\frac{3}{2}}\right)$
$\Rightarrow \cos\beta\approx0.9$
So, angle $\beta$ is not more than $30°.$