Q.
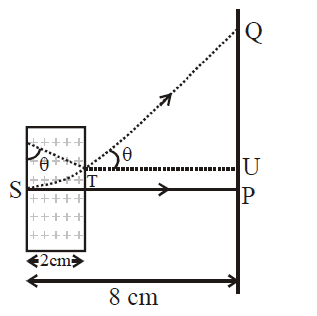
An electron, moving along the x-axis with an initial energy of $100\, eV$, enters a region of magnetic field $\vec{B} \, = (1.5 \times 10^{-3} T) \hat{k}$ at $S$ (See figure). The field extends between $x = 0$ and $x = 2\, cm$. The electron is detected at the point $Q$ on a screen placed $8\, cm$ away from the point $S$. The distance $d$ between $P$ and $Q$ (on the screen) is : (electron's charge = $1.6 \times 10^{-19}C.$ mass of electron = $9.1 \times 10^{-31}kg)$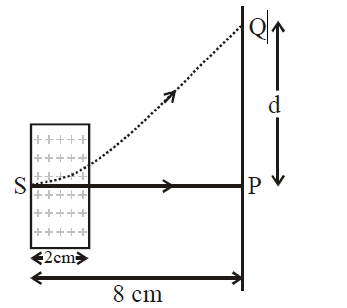
Solution:
$R = \frac{mv}{qB}$
$= \frac{\sqrt{2m (K.E.)}}{qB}$
$R = \frac{\sqrt{2 \times 9.1 \times 10^{-31} \times(100 \times 1.6 \times 10^{-19}}}{1.6 \times 10^{-19} \times 1.5 \times 10^{-3}}$
$R = 2.248$ cm
$sin \theta = \frac{2}{2.248}$
$tan \theta = \frac{QU}{TU}$
$\frac{2}{1.026} \, = \, \frac{QU}{6}$
$QU = 11.69$
$PU = R(1 - cos \theta)$
= $1.22$
$d = QU + PU$