Q.
An electric dipole with dipole moment $\frac{p_{0}}{\sqrt{2}}\left(\hat{i}+\hat{j}\right)$ is held fixed at the origin O in the presence of an uniform electric field of magnitude E0. If the potential is constant on a circle of radius R centered at the origin as shown in figure, then the correct statement(s) is/are:
($\varepsilon_{0}$ is permittivity of free space, R >> dipole size)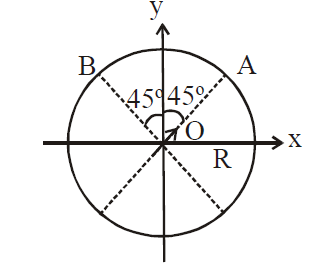
Solution:
$\left(1\right) \overrightarrow{P} = \frac{P_{0}}{\sqrt{2}}\left(\hat{i} +\hat{j}\right)$
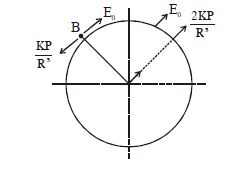
E.F. at B along tangent should be zero since circle is equipotential.
So, $E_{0} = \frac{K\left|\vec{P}\right|}{R^{3}} \& E_{B} = 0$
So, $R^{3} = \frac{KP_{0}}{E_{0}} = \left(\frac{P_{0}}{4\pi\,\in_{0}\,E_{0}}\right)$
So $R = \left(\frac{P_{0}}{4\pi \,\in _{0}\,E_{0}}\right)^{1/3}$
So, (1) is correct
(2) Because $E_{0}$ is uniform & due to dipole E.F. is different at different points, so magnitude of total E.F. will also be different at different points.
So, (2) is incorrect
$\left(3\right) E_{A} = \frac{2KP}{R^{3}} + \frac{KP}{R^{3}} = 3 \frac{KP}{R^{3}} \frac{P_{0}}{\sqrt{2}}\left(\hat{i} + \hat{j}\right)$
So,t(3) is wrong
$\left(4\right) E_{B} = 0$
so, (4) is correct