1. Tardigrade
  2. Question
  3. Physics
  4. An electric dipole has a fixed dipole moment vecp, which makes angles θ with respect to x-axis. When subjected to an electric field vecE1 = E hati, it experiences a torque vecT1 = τ hatk. When subjected to another electric field vecE2 = √3 E1 hatj it experiences a torque vecT2 = - vecT1. The angle θ is

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

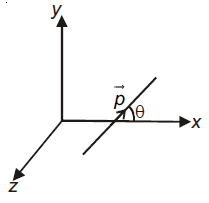
Q. An electric dipole has a fixed dipole moment $\vec{p}$, which makes angles $\theta$ with respect to x-axis. When subjected to an electric field $\vec{E}_1 = E \hat{i}$, it experiences a torque $\vec{T}_1 = \tau \hat{k}$. When subjected to another electric field $\vec{E}_2 = \sqrt{3 E_1} \hat{j}$ it experiences a torque $\vec{T}_2 = - \vec{T}_1$. The angle $\theta$ is

JEE MainJEE Main 2017Electric Charges and Fields

Solution:

$\vec{p} = p \cos \theta \hat{i} + p \sin \theta \hat{j}$
$\vec{E}_1 = E \hat{i}$
$\vec{T}_1 = \vec{p} \times \vec{E}_1$
$ = (p \cos \theta \hat{i} + p \sin \theta \hat{j} ) \times E (\hat{i})$
$\tau \hat{k} = p E \sin \theta (- \hat{k})$ ......(i)
$\vec{E}_2 = \sqrt{3} E_1 \hat{j}$
$\vec{T}_2 = (p\cos \theta \hat{i} + p \sin \theta \hat{j} ) \times \sqrt{3} E_1 \hat{j}$
$ - \tau \hat{k} = \sqrt{3} p E_1 \cos \theta \hat{k}$ ....(ii)
From (i) and (ii)
$p E \sin \theta = \sqrt{3} pE \cos \theta$
$\tan \theta = \sqrt{3}$
$\theta = 60^{\circ}$

Solution Image