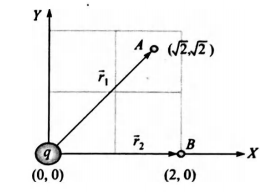
Question

An electric charge $10^{-3} \mu C$ is placed at the origin $(0, 0)$ of $x-y$ coordinate system. Two points $A$ and $B$ are situated at $(\sqrt{2}, - \sqrt{2})$ and $(2,0)$, respectively. The potential difference (in $V$) between the points $A$ and $B$ will be _________.

Answer 1

The position vector of $A, \vec{r}_1 = \sqrt{2}\hat{i} + \sqrt{2} \hat{j}$
$|\vec{r}_1| = r_1 = \sqrt{(\sqrt{2})^2 + (\sqrt{2})^2} = 2$

The position vector of $B, \vec{r}_2 = 2\hat{i} + 0 \hat{j}$
or $|\vec{r}_2| = r_2 = 2$
Potential at point $A$ is:
$V_A = \frac{1}{4\pi \varepsilon_0} \frac{q}{r_1} = \frac{1}{4\pi \varepsilon_0} \frac{10^{-3} \times 10^{-6}}{2}$
Potential at point $B$ is:
$V_B = \frac{1}{4\pi\varepsilon_0} \frac{q}{r_2} = \frac{1}{4\pi\varepsilon_0} \frac{10^{-3} \times 10^{-6}}{2}$