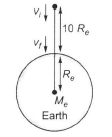
Q. An asteroid of mass m is approaching earth, initially at a distance of 10$R_e$, with speed $v_i$. It hits the earth with a speed $v_f$ ($R_e$ and $M_e$ are radius and mass of earth), then
Gravitation
Solution:
Applying law of conservation of energy for asteroid at a distance $10\, R_e$ and at earth's surface,
$K_i + U_i = K_f + U_f ...(i)$
Now, $K_i = \frac{1}{2}mv^2_i $ and $U_i = \frac{GM_e m}{10 R_e}$
$K_f = \frac{1}{2}mv^2_f $ and $U_f = \frac{GM_e m}{R_e}$
Substituting these values in Eq. (i), we get
$\frac{1}{2}mv_i^2 -\frac{GM_e m}{10R_e} =\frac{1}{2}mv^2_f - \frac{GM_e m}{R_e}$
$\Rightarrow \frac{1}{2}mv_f^2 =\frac{1}{2}mv^2_i +\frac{GM_e m}{R_e}-\frac{GM_e m}{10R_e}$
$\Rightarrow v_f^2 =v^2_i +\frac{2GM_e}{R_e}-\frac{2GM_e}{10R_e}$
$\therefore v_f^2 =v^2_i +\frac{2GM_e}{R_e}\left(1-\frac{1}{10}\right)$