Question

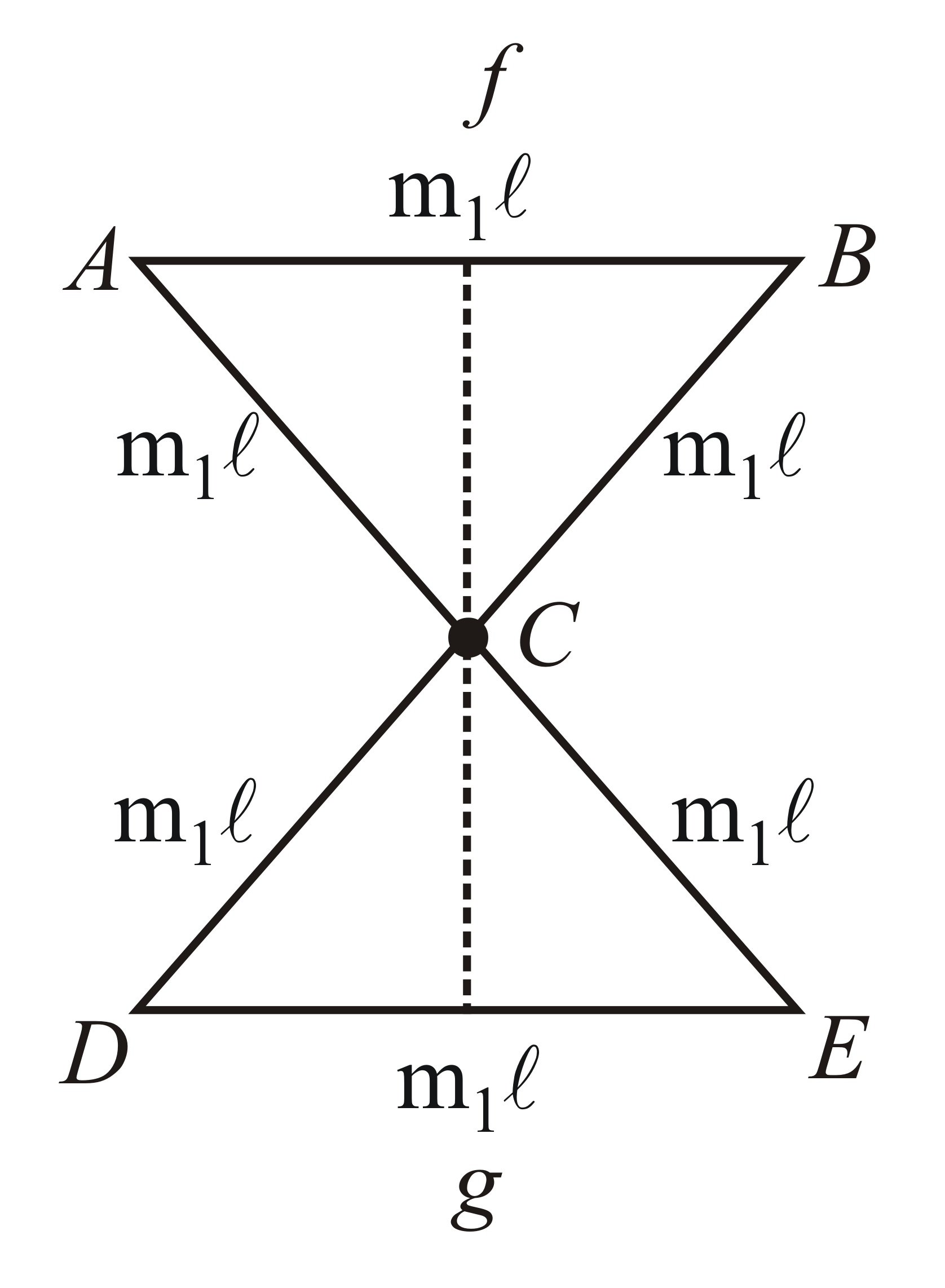
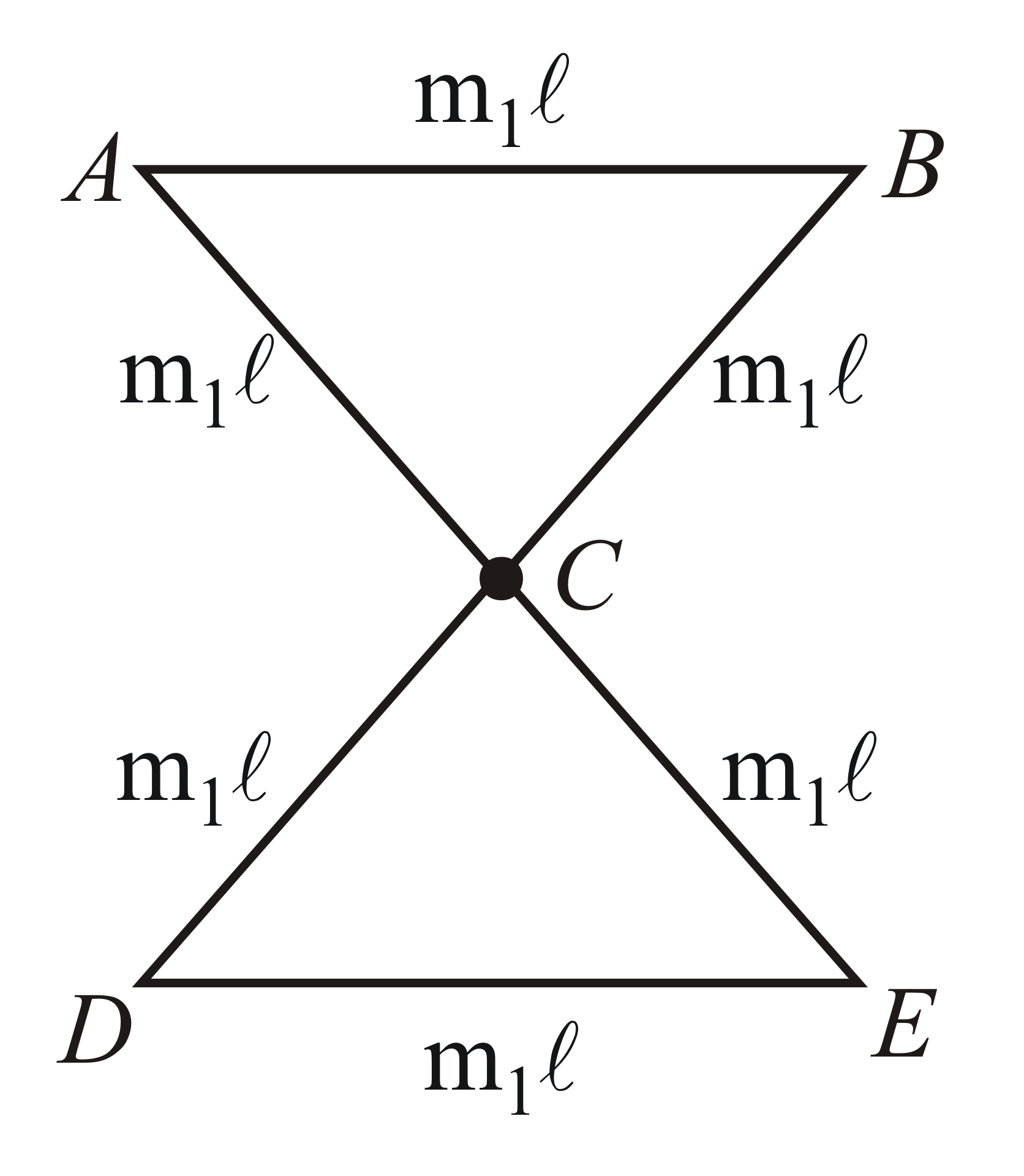
An arrangement of rods, each of mass $m$ and length $l$ are welded (wherever required) to form a shape as shown. The moment of inertia about an axis passing through point $C$ and perpendicular to the plane of figure is,

• A. $ml^{2}$
• B. $\frac{3}{2}ml^{2}$
• C. $3ml^{2}$
• D. $\frac{9}{2}ml^{2}$

Answer 1

Answer: (C)

Moment of inertia of a rod of mass $m$ And length $l$ about its end is $\frac{m l^{2}}{3}$
Moment of inertia of a rod of mass $m$ And length $l$ about its centre is $\frac{m l^{2}}{12}$
Moment of Inertia of the given system about Point $C$ and perpendicular to plane can be calculated as

$I=I_{A C}+I_{B C}+I_{C D}+I_{D E}+I_{A B}+I_{D E}I=\frac{m l^{2}}{3}+\frac{m l^{2}}{3}+\frac{m l^{2}}{3}+\frac{m l^{2}}{3}+I_{A B}+I_{D E}..\left(1\right)$
Let's calculate Moment of inertia of $AB\&DE$ Using parallel axis theorem
$I_{A B}=I_{f}+m\left(c f\right)^{2}I_{A B}=\frac{m l^{2}}{12}+m\frac{3 l^{2}}{4}$
$I_{D E}=I_{g}+m\left(c g\right)^{2}I_{D E}=\frac{m l^{2}}{12}+m\frac{3 l^{2}}{4}$
Substituting the values of $I_{A B}\&I_{D E}$ in equation first we have
$I=\frac{m l^{2}}{3}+\frac{m l^{2}}{3}+\frac{m l^{2}}{3}+\frac{m l^{2}}{3}+I_{A B}+I_{D E}I=\frac{4 m l^{2}}{3}+2\left[\frac{m l^{2}}{12} + \frac{3 m l^{2}}{4}\right]=3ml^{2}$