Q.
An archer shoots an arrow from a height $4.2\, m$ above the ground with a speed $40 \,m / s$ and at an angle $30^{\circ}$ as shown in the figure. Determine the horizontal distance $R$ covered by the arrow, when it hits the ground, $\left(\right.$ Take $\left.g=10\, m / s ^{2}\right)$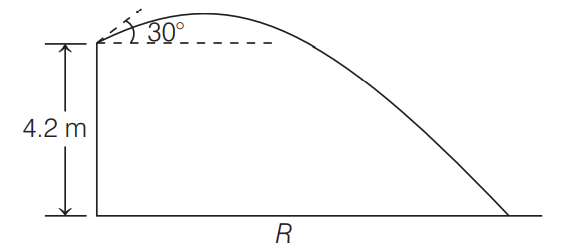
TS EAMCET 2019
Solution:
