Q.
An aluminium wire of length $l_{1}=60.0\, cm$ of cross-sectional area $1.00 \times 10^{-2} cm ^{2}$ is connected to a steel wire of the same cross-sectional area. The compound wire, loaded with a block $m$ of mass $10.0\, kg$ (as in fig), so that the distance $l_{2}$ from the joint to the supporting pulley is $86.6 cm$. Transverse waves are set up in the wire by using an external source of variable frequency. What is the lowest frequency of excitation for which standing waves are observed such that the joint in the wire is a node?
(Take $g =1000\, cm / s ^{2}$ ] $\left[\rho_{ Al }=2.6 g / cm ^{3}\right.$;
$\rho_{\text {steel }}=7.8\, g / cm ^{3}$ )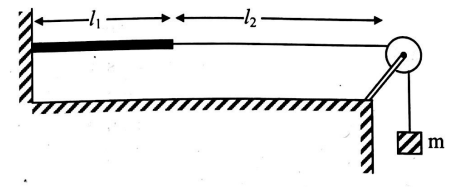
Waves
Solution:
