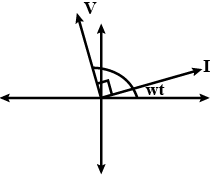
Q. An alternating voltage $V=V_{0} \sin \omega t$ is applied across a circuit. As a result, a current $I=I_{0} \sin (\omega t-\pi / 2)$ flows in it. The power consumed per cycle is
BITSATBITSAT 2010
Solution:
In the circuit, voltage $V = V _{0} \sin \omega t$ and current
$I = T _{0} \sin \left(\omega t -\frac{\pi}{2}\right)$
Phase different between voltage and current at any time would be
$\phi=\frac{\pi}{2}$ (from phasor diagram)
So power consumed,
$P =\frac{ I _{0} V _{0}}{2} \cos \phi$
$=\frac{ I _{0} V _{0}}{2} \cos \left(\frac{\pi}{2}\right)$
$= P =0$