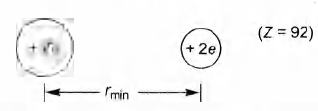
Q. An alpha particle of energy $5 \,MeV$ is scattered through $180^\circ$ by a fixed uranium nucleus. The distance of closest approach is of the order of
IIT JEEIIT JEE 1981Nuclei
Solution:
From conservation of mechanical energy decrease in kinetic energy = increase in potential energy or $\frac{1}{4 \pi \varepsilon_0} \frac{(Ze)(Ze)}{r_{min}}=5\, MeV=5 \times 1.6 \times10^{-13}\, J $
$\therefore \, \, \, r_{min}=\frac{1}{4 \pi \varepsilon_0}\frac{2Ze}{5 \times 1.6 \times10^{-13}} $
$ = \frac{(9 \times 10^9) (2)(92)(1.6 \times 10^{-19})^2}{5 \times 1.6 \times10^{-13}} $
$ = 5.3 \times 10^{-14}\, m= 5.3 \times 10^{-12} cm$
i.e.$r_{min}$ is of the order of $10^{-12} cm$