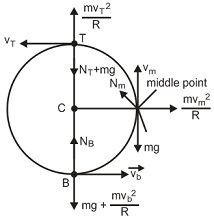
Question

An aircraft loops a vertical loop of radius $R \, = \, 500 \, m$ with a constant velocity $v=360 \, kmh^{- 1}$ . Find the weight of the flier of mass $m=70 \, kg$ in the lower, upper, and middle points of the loop.

• A. $2.1kN,0.7kN,1.5kN$
• B. $0.7kN,1.5kN,2.1kN$
• C. $1.5kN,2.1kN,0.7kN$
• D. none of these

Answer 1

Answer: (A)

Forces on the flier in the frame of aircaraft (non inertial reference frame) is:
(i) Normal reaction (N)
(ii)Pseudo force $\left(\frac{m v^2}{R}\right)$
(iii) Gravitational force d(mg)
According to problem,
v_T = v_b = v_m = v
The net force on flier at every point should be zero in the frame of aircraft. For top point T,
$N_{T} + \text{mg} = \frac{ mv _{\text{T}}^{2}}{ R ⁡} \therefore N_{T} = \frac{mv ⁡^{2}}{ R ⁡} - \text{mg}$
= 0.7 kN
For bottom point, $ N _{ B ⁡} = \text{mg} + \frac{ mv ⁡_{b}^{2}}{ R ⁡} = \text{mg} + \frac{ mv ⁡^{2}}{ R ⁡}$
= 2.1 kN.

For middle point, $N_{m} = \sqrt{\left(\frac{\text{mv}_{}^{2}}{R}\right)^{2} + \left(\text{mg}\right)^{2}} = 1 \text{.} 5 k N $