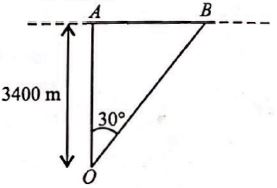
Question

An aircraft is flying at a height of $3400\, m$ above the ground. If the angle subtended at a ground observation point by the aircraft positions $10\,s$ apart is $30^\circ$ then the speed of the aircraft is

• A. $ 19.63\,m{{s}^{-1}} $
• B. $ 196.3\,m{{s}^{-1}} $
• C. $ 108\,m{{s}^{-1}} $
• D. $ 1963\,m{{s}^{-1}} $
• E. $ 10.8\,m{{s}^{-1}} $

Answer 1

Answer: (B)

$O$ is the observation point at the ground. $A$ and $B$ are the positions of aircraft for which $\angle AOB=30^°$.
Time taken by aircraft from $A$ to $B$ is $10\,s$.
In $\Delta AOB,$
$\tan\,30^{\circ}$
$=\frac{AB}{3400}$
$AB=3400\,\tan\,30^{\circ}$
$=\frac{3400}{\sqrt{3}}m$
$\therefore $ Speed of aircraft, $v=\frac{AB}{10}$
$=\frac{3400}{10\sqrt{3}}$
$=196.3\,ms^{-1}$