1. Tardigrade
  2. Question
  3. Physics
  4. An aeroplane flies around a square field ABCD of each side 1000 km. Its speed along AB is 250 text kmh-1, along BC 500 text kmh-1, along CD 200kmh-1, and along DA 100 text kmh-1 . Its average speed (in kmh-1 )over the entire trip is

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

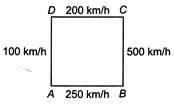
Q. An aeroplane flies around a square field $ABCD$ of each side $1000\, km$. Its speed along $AB$ is $ 250\text{ }km{{h}^{-1}}, $ along $BC$ $ 500\text{ }km{{h}^{-1}}, $ along $CD$ $ 200km{{h}^{-1}}, $ and along $DA$ $ 100\text{ }km{{h}^{-1}} $ . Its average speed (in $ km{{h}^{-1}} $ )over the entire trip is

KEAMKEAM 2010Motion in a Plane

Solution:

Time along the $ AB=\frac{1000}{250}=4\text{ }h $
Time along the $ BC=\frac{1000}{500}=2\text{ }h $
Time along the $ CD=\frac{1000}{200}=5\text{ }h $
Time along the $ AD=\frac{1000}{100}=10\text{ }h $
Average speed $ =\frac{Total\,dis\tan ce}{Total\,time} $
$ =\frac{4\times 1000}{4+2+5+10}=\frac{4000}{21} $
$ =190.5\text{ }km/h $

Solution Image