Question

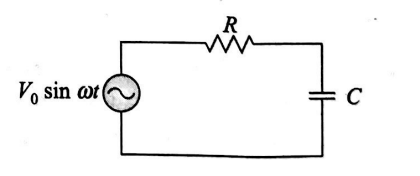
An ac voltage source $V=V_{0} \sin \omega t$ is connected across resistance $R$ and capacitance $C$ as shown in figure. It is given that $R=1 / \omega C$. The peak current is $I_{0}$. If the angular frequency of the voltage source is changed to $\omega / \sqrt{3}$ then the new peak current in the circuit is

• A. $\frac{I_{0}}{2}$
• B. $\frac{I_{0}}{\sqrt{2}}$
• C. $\frac{I_{0}}{\sqrt{3}}$
• D. $\frac{I_{0}}{3}$

Answer 1

Answer: (B)

The peak value of the current is
$I_{0} \frac{V_{0}}{\sqrt{R^{2}+\frac{1}{\omega^{2} C^{2}}}}=\frac{V_{0}}{\sqrt{2} R}$
when the angular frequency is changed to $\frac{\omega}{\sqrt{3}}$ The new peak value is
$ I_{0}^{\prime}=\frac{V_{0}}{\sqrt{R^{2}+\frac{3}{\omega^{2} C^{2}}}}=\frac{V_{0}}{\sqrt{4 R^{2}}}=\frac{V_{0}}{2 R} $
$\therefore I_{0}^{\prime} =\frac{I_{0}}{\sqrt{2}}$