Q.
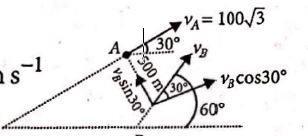
Airplanes $A$ and $B$ are flying with constant velocity in the same vertical plane at angles $30^°$ and $60^°$ with respect to the horizontal as shown in figure. The speed of $A$ is $100\sqrt{3}\,ms^{-1}$. At time $t = 0\,s$, an observer in $A$ finds $B$ at a distance of $500\,m$. This observer sees $B$ moving with a constant velocity perpendicular to the line of motion of $A$. If at $t = t_0$, $A$ just escapes being hit by $B$, $t_0$ is
Motion in a Plane
Solution:
The relative velocity of $B$ with respect to $A$ is perpendicular to the line of motion of $A$.
$\therefore v_{B}cos30^{°}=v_{A}$
$v_{B}=\frac{v_{A}}{cos\,30^{°}}$
$=\frac{100\sqrt{3}}{\sqrt{3}/2}200\,ms^{-1}$
$\therefore t_{0}=\frac{500}{v_{B}\,sin\,30^{\circ}}$
$=\frac{500}{200\times\frac{1}{2}}=5\,s$