Question

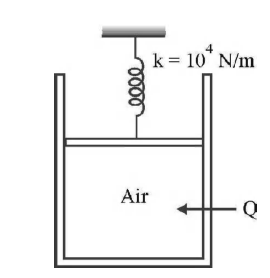
Air is contained in a piston - cylinder arrangement as shown in Fig. with a cross - sectional area of $4$ cm$^{2}$ and an initial volume of $20\, cc$. The air is initially at a pressure of $1\, atm$ and temperature of $20^{\circ}C$. The piston is connected to a spring whose spring constant is $k = 10^4 \,N/m$, and the spring is initially undeformed. How much heat (in joule) must be added to the air to increase the pressure to $3$ atm. (For air, $C_{V}— 718 J/kg^{\circ}C$, molecular mass of air $28.97$)

Answer 1

When pressure changes from 1 atm to 3 atm , the change in pressure $P = 2$ atm
$= 2\times 1 \times 10^{5}N/m^{2}$
The force exerted on the piston
$ F = PA = 2 \times10^{5} \times 4 \times 10^{-4}$
$ = 80 N$
The compression of the spring
$x =\frac{F}{k} = \frac{80}{10^{4}} = 0.008$ m
The change in volume of the air due to displacement of piston by $x$
$\Delta V = Ax = 4\times10^{-4} \times0.008$
$= 3.2 \times10^{-6} m^{3}$
$\therefore $ Final volume $V_{2} = V_{1} +\Delta V$
$= 20 \times10^{-6} +3.2\times10^{-6}$
$= 23.2 \times10^{-6}m^{3}$
By equation of state
$\frac{P_{1}V_{1}}{T_{1}} = \frac{P_{2}V_{2}}{T_{2}}$
$T_{2} = \frac{P_{2}V_{2}T_{1}}{P_{1}V_{1}}$
$= \left(\frac{3}{1}\right) \times\frac{\left(23.2 \times10^{-6}\right)}{\left(20\right) \times10^{-6}} \times\left(273 +20\right)$
$= 1020K$
The change in internal energy of air
$\Delta U = m C_{V}\Delta T$
$ = \left(2.38 \times10^{-5}\right) \times718 \times\left(1020 -293\right)$
$ = 12.42J$ Work done in compressing the spring by $x$
$W = \frac{1}{2}kx^{2} = \frac{10^{4}}{2} \times\left(0.008\right)^{2} = 0.32J$
From first law of thermodynamics
$Q =\Delta U + W = 12.42 +0.32 =12.74J$