Q.
A conical pendulum consists of a simple pendulum moving in a horizontal circle as shown in the figure. $C$ is the pivot, $O$ the centre of the circle in which the pendulum bob moves and $\omega$ the constant angular velocity of the bob. If $\vec{L}$ is the angular momentum about point $C$, then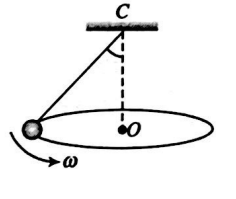
System of Particles and Rotational Motion
Solution: