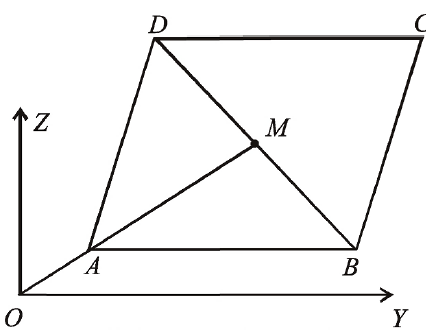
Q. $ABCD$ is parallelogram. The position vectors of $A$ and $C$ are respectively, $3\hat{i}+3\hat{j}+5\hat{k}$ and $\hat{i}-5\hat{j}-5\hat{k}.$ If $M$ is the midpoint of the diagonal $DB$, then the magnitude of the projection of $\overrightarrow{OM}$ on $\overrightarrow{OC}$, where $O$ is the origin, is
AIEEEAIEEE 2012Vector Algebra
Solution:
In a parallelogram, diagonals bisect each other. So, mid point of $DB$ is also the midpoint of $AC$.
Mid-point of $M=2\hat{i}-\hat{j}$
Direction ratio of $OC = \left(1, - 5, - 5\right)$
Direction ratio of $OM = \left(2, -1,0\right)$
Angle \theta between $OM$ and $OC$ is given by
$cos\,\theta=\frac{\left(1\times2+\right)-5\left(-1\right)\left(+-5\right)0\left(\right)\left(\right)}{\sqrt{2^{2}+\left(-1\right)^{2}}\sqrt{\left(1\right)^{2}+\left(-5\right)^{2}+\left(-5\right)^{2}}}$
$=\frac{2+5}{\sqrt{5}\sqrt{51}}=\frac{7}{\sqrt{5}\sqrt{51}}$
Projection of $\overrightarrow{OM}$ on $\overrightarrow{OC}$ is given by
$\left|OM\right|.cos\,\theta=\sqrt{5}\times\frac{7}{\sqrt{5}\times\sqrt{51}}=\frac{7}{\sqrt{51}}$