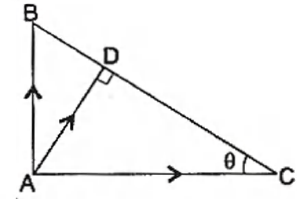
Q. $A B C$ is a triangle, right angled at $A .$ The resultant of the forces acting along $\overline{A B}, \overline{B C}$ with magnitudes $\frac{1}{A B}$ and $\frac{1}{A C}$ respectively is the force along $\overline{A D},$ where $D$ is the foot of the perpendicular from $A$ onto $B C$. The magnitude of the resultant is
AIEEEAIEEE 2006Vector Algebra
Solution:
Let $\left|\overrightarrow{BC}\right|=l$
$\therefore In\,\Delta\Lambda ABC,$
$l=\sqrt{AB^{2}+AC^{2}}$
and $tan \,\theta=\frac{AB}{AC}$
$\Rightarrow sin\,\theta=\frac{AB}{l}$ and $cos\,\theta=\frac{AC}{l}$
$\therefore $ Resultant vector
$\frac{1}{AB} \hat{i}+\frac{1}{AC} \hat{j}=\left(\frac{1}{l\,sin\,\theta} \hat{i}+\frac{1}{l\,cos\,\theta} \hat{j}\right)$
$=k\,\overrightarrow{AD}$
Now, $AD=AC\,sin\,\theta=l\,sin\,\theta\,cos\,\theta$
$=\frac{AB\cdot AC}{l}$
Magnitude of resultant vector
$=\sqrt{\frac{1}{l^{2}}\left(\frac{1}{sin^{2}\,\theta}+\frac{1}{cos^{2}\,\theta}\right)}$
$=\frac{l}{\left(AB\right)\left(AC\right)}=\frac{1}{AD}$