Q.
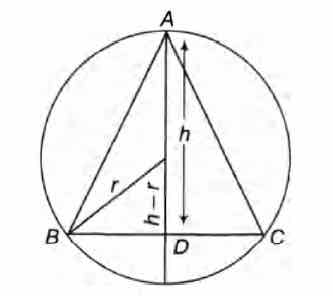
ABC is an isosceles triangle inscribed in a circle of radius
r. If A B = A C and h is the altitude from A to BC, then the
$\triangle ABC$ has perimeter P = 2 $ ( \sqrt{2 hr - h^2} + \sqrt{2hr})$ and area
A = .... , Also, $ lim_{ h \to 0 } \frac{A}{ P^3}$ = ....
IIT JEEIIT JEE 1989
Solution:
P = 2 $ ( \sqrt{2 hr - h^2} + \sqrt{2hr})$
Here, BD = $ \sqrt{ r^2 - (h - r)^2 } = \sqrt{ 2hr - h^2} $
$\therefore A = \frac{1}{2} . 2BD. h = ( \sqrt{ 2hr - h^2}) $ h
$\therefore lim_{h \to 0 } \frac{A}{P^3} = lim_{h \to 0} \frac{ h \sqrt{ 2hr - h^2}}{ 8 ( \sqrt {2 hr - h^2 } + \sqrt{ 2hr})^3} $
= $ lim_{ h \to 0 } \frac{ h^{3/2} (\sqrt{2r - h})}{ 8 \, h^{3/2} (\sqrt{ 2 r - h } + \sqrt{ 2r})^3 }$
= $ \frac{1}{8}. \frac{ \sqrt{2r}}{ (\sqrt{2r} + \sqrt{2r})^3 } $
= $ \frac{1}{128 \, r} $