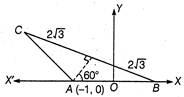
Q. ABC is an isosceles triangle in which A is $ (-1,0), $ $ \angle A=\frac{2\pi }{3},\text{ }AB=AC $ and AB is along the $ x- $ axis. If $ BC=4\sqrt{3}, $ then the equation of the line BC is
JamiaJamia 2013
Solution:
$ (1+OB)\cos 30{}^\circ =2\sqrt{3} $ $ \Rightarrow $ $ 1+OB+2\sqrt{3}\times \frac{2}{\sqrt{3}}=4 $
$ \Rightarrow $ $ OB=3 $ $ \Rightarrow $ $ B=(3,0) $ and $ m $ of $ BC=\tan 150{}^\circ =-\frac{1}{\sqrt{3}} $ So, the equation of $ BC $ is $ y-0=-\frac{1}{\sqrt{3}}(x-3) $ i.e., $ x+\sqrt{3}y=3 $