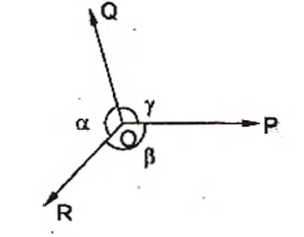
Q. $ABC$ is a triangle. Forces $\vec{P}, \vec{Q}, \vec{R}$ acting along $IA, IB$ and $IC$ respectively are in equilibrium, where $I$ is the in centre of $\Delta \, ABC$. Then $\vec{P} : \vec{Q} : \vec{R}$ is :
AIEEEAIEEE 2005
Solution:
If three forces acting on a particle keep it in equilibrium, each is proportional to the sine of the angle between the other two.
$\therefore \frac{P}{\sin\,\alpha}=\frac{Q}{\sin\,\beta}=\frac{R}{\sin\,\gamma}$
This theorem is known as Lami’s theorem.
In a $\Delta \, ABC, I$ is the in centre.
$\therefore \angle \,BIC$$=\pi-\left(\frac{B}{2}+\frac{C}{2}\right)$
$=\pi-\left(\frac{\pi}{2}-\frac{A}{2}\right)$
$=\frac{\pi }{2}+\frac{A}{2}$
Similarly, $\angle\, AIC$ $\frac{\pi }{2}+\frac{B}{2}$ and $\angle\, AIB \frac{\pi }{2}+\frac{C}{2}$
By Lami’s theorem
$\frac{\vec{A}}{\sin\,BIC}=\frac{\vec{B}}{\sin\,AIC}\frac{\vec{R}}{\sin\,AIB}$
$\therefore \vec{P} : \vec{Q} : \vec{R}$
$=\sin \left(\frac{\pi}{2}+\frac{A }{2}\right) : \left(\frac{\pi }{2}+\frac{B }{2}\right) : \sin \left(\frac{\pi }{2}+\frac{C }{2}\right)$
$=\cos \frac{A}{2} :\cos \frac{B}{2} : \cos \frac{C}{2} $