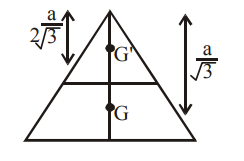
Question

$ABC$ is a plane lamina of the shape of an equilateral triagnle. $D , E$ are mid points of $AB$ $AC$ and $G$ is the centroid of the lamina. Moment of inertia of the lamina about an axis passing through $G$ and perpendicular to the plane $ABC$ is $I_{0}$. If part ADE is removed, the moment of inertia of the remaining part about the same axis is $\frac{ NI _{0}}{16}$ where $N$ is an integer. Value of $N$ is _______.

Answer 1

Let side of triangle is a and mass is $m$

MOI of plate $ABC$ about centroid
$I_{0}=\frac{ m }{3}\left(\left(\frac{ a }{2 \sqrt{3}}\right)^{2} \times 3\right)=\frac{ ma ^{2}}{12}$
triangle ADE is also an equilateral triangle of side $a / 2$
Let moment of inertia of triangular plate ADE about it's centroid (G') is $I_{1}$ and mass is $m_{1}$
$m _{1}=\frac{ m }{\frac{\sqrt{3} a ^{2}}{4}} \times \frac{\sqrt{3}}{4}\left(\frac{ a }{2}\right)^{2}=\frac{ m }{4}$
$I_{1}=\frac{m_{1}}{12}\left(\frac{a}{2}\right)^{2}=\frac{m}{4 \times 12} \frac{a^{2}}{4}=\frac{m a^{2}}{192}$

distance $GG'=\frac{ a }{\sqrt{3}}-\frac{ a }{2 \sqrt{3}}=\frac{ a }{2 \sqrt{3}}$
so MOI of part ADE about centroid G is
$I _{2}= I _{1}+ m _{1}\left(\frac{ a }{2 \sqrt{3}}\right)^{2}$
$=\frac{ ma ^{2}}{192}+\frac{ m }{4} \cdot \frac{ a ^{2}}{12}$
$=\frac{5 ma ^{2}}{192}$
now MOI of remaining part
$=\frac{m a^{2}}{12}-\frac{5 m a^{2}}{192}$
$=\frac{11 m a^{2}}{12 \times 16}=\frac{11 I_{0}}{16} $
$\Rightarrow N=11$