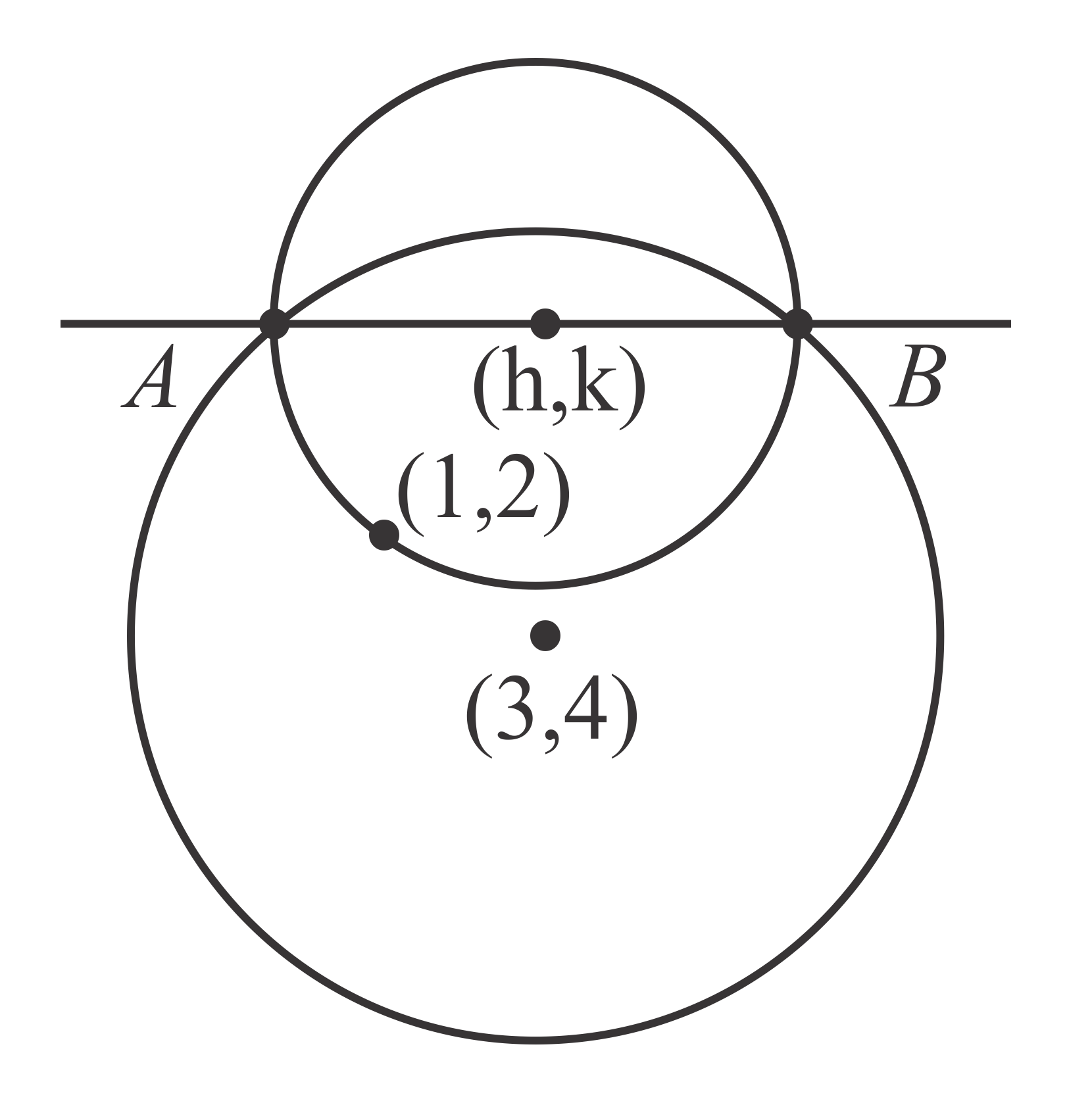Question

$AB$ is any chord of the circle $x^{2}+y^{2}-6x-8y-11=0,$ which subtends $90^\circ $ at $\left(1 , 2\right)$ . If locus of mid-point of $AB$ is a circle $x^{2}+y^{2}-2ax-2by-c=0,$ then value of $\left(a + b + c\right)$ is

Answer 1

Let $\left(h , k\right)$ be the mid-point of chord $AB$ .
$\left(x - h\right)^{2}+\left(y - k\right)^{2}=\left(h - 1\right)^{2}+\left(k - 2\right)^{2}$
$\Rightarrow \, \, x^{2}+y^{2}-2hx-2ky+2h+4k-5=0...\left(1\right)$
Given equation of circle is
$x^{2}+y^{2}-6x-8y-11=0...\left(2\right)$
$\Rightarrow \, \, $ Equation of chord is $\left(1\right),\left(2\right)$
$\left(h - 3\right)x+\left(k - 4\right)y-h-2h-3=0...\left(3\right)$
Equation of chord w.r.t. midpoint is $T=S_{1}$
$xh+ky-3\left(x + h\right)-4\left(y + k\right)-11$
$=h^{2}+k^{2}-6h-8k-11...\left(4\right)$
Comparing $\left(3\right)$ and $\left(4\right)$
$3h+4k-h^{2}-k^{2}=-h-2k-3$
$\Rightarrow \, \, h^{2}+k^{2}-4h-6k-3=0$
$\therefore \, \, a=2;b=3;c=3$
$\therefore \, a+b+c=8$