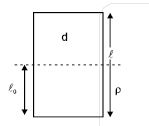
Q. A wooden cube (density of wood $'d'$) of side $'\ell'$ floats in a liquid of density $'\rho'$ with its upper and lower surfaces horizontal. If the cube is pushed slightly down and released, it performs simple harmonic motion of period $'T'$. Then, $'T'$ is equal to :
AIEEEAIEEE 2011Oscillations
Solution:
At equilibrium
$F_{b} = mg$
$\rho A\ell_{0}g = dA\ell g \quad...........\left(i\right)$
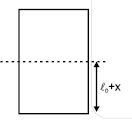
Restoring force,
$F = mg - F_{b}'$
$F = mg - \rho A\left(\ell_{0} + x\right)g$
$dA\ell a = dA\ell g - \rho A\ell_{0}g - \rho gAx$
$a = \frac{\rho g}{d\ell}x$
$\omega = \sqrt{\frac{\rho g}{d\ell}}$
$T = 2\pi\sqrt{\frac{\ell d}{\rho g}}\quad...........\left(i\right)$