Question

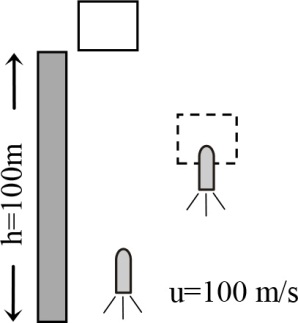
A wooden block of mass $10 \, gm$ is dropped from the top of a tower $100 \, m$ high. Simultaneously, a bullet of mass $10 \, gm$ is fired from the foot of the tower vertically upwards with a velocity of $100ms^{- 1}$ . If the bullet is embedded in it, how high will it rise above the tower before it starts falling? $\left(g = 10 m s^{- 2}\right)$

Answer 1

Block and bullet will collide after $1 \, s$ at height $95 \, m$ from ground.
$Velocity \, of \, block \, before \, collision=gt=10 \, ms^{- 1}$
$Velocity \, of \, bullet \, before \, collision=u-gt=90 \, ms^{- 1}$
from conservation of linear momentum,
$m\left(- 10\right)+m\left(90\right)=2 \, mv′ \, \Rightarrow \, v′=40 \, ms^{- 1}$


Thus height raised by the combined mass
$h=\frac{v ′^{2}}{2 g}=\frac{40 \times 40}{2 \times 10}=80 \, m$
$height \, from \, tower=75 \, m$