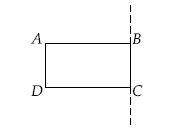
Question

A wire of length l and mass m is bent in the form of a rectangle $ABCD$ with $\frac{AB}{BC}=2.$ The moment of inertia of this wire frame about the side $BC$ is

• A. $\frac{11}{252}ml^{2}$
• B. $\frac{8}{203}ml^{2}$
• C. $\frac{5}{136}ml^{2}$
• D. $\frac{7}{162}ml^{2}$

Answer 1

Answer: (D)

$\frac{AB}{BC}=2 \,\therefore AB=DC=\frac{l}{3}$
and $BC=AD=\frac{l}{6}$
Similarly, $m_{AB}=m_{Dc}=\frac{m}{3}$
and $m_{BC}=m_{AD}=\frac{m}{6}$
$\therefore $ Moment of inertia of the wire frame about the given axis is
$I=I_{AB}+I_{AD}+I_{Dc}+I_{BC}$
$=\frac{1}{3}\left(\frac{m}{3}\right)\left(\frac{l}{3}\right)^{2}+\left(\frac{m}{6}\right)\left(\frac{l}{3}\right)^{2}+\frac{1}{3}\left(\frac{m}{3}\right)\left(\frac{l}{3}\right)^{2}+0$
$=\frac{ml^{2}}{81}+\frac{ml^{2}}{54}+\frac{ml^{2}}{81}=\frac{7}{162}ml^{2}$