Q.
A wire, of length $L(= 20 \,cm)$, is bent into a semi-circular arc. If the two equal halves, of the arc, were each to be uniformly charged with charges $\pm Q, [ | Q | = 10^3 \varepsilon_{0}$ Coulomb where $\varepsilon_{0}$ is the permittivity (in SI units) of free space] the net electric field at the centre $O$ of the semicircular arc would be :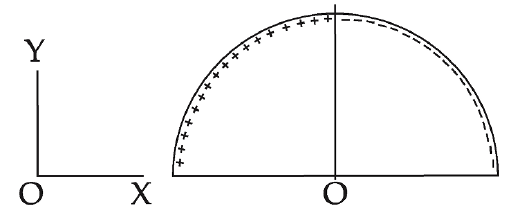
Solution:
