Question

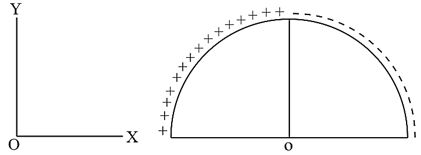
A wire of length $L=20 \, cm$ is bent into a semi-circular arc and the two equal halves of the arc are uniformly charged with charges $+Q$ and $-Q$ as shown in the figure. The magnitude of the charge on each half is $\left|Q\right|=10^{3}\epsilon _{0}$ , where $\epsilon _{0}$ is the permittivity of free the space. The net electric field at the centre $O$ is

• A. $\left(25 \times 10^3\right) \hat{\mathrm{i}} \quad \mathrm{NC}^{-1}$
• B. $\left(50 \times 10^3\right) \hat{\mathrm{i}} \quad \mathrm{NC}^{-1}$
• C. $\left(25 \times 10^3\right) \hat{j} \quad \mathrm{NC}^{-1}$
• D. $\left(50 \times 10^3\right) \hat{\mathrm{j}} \quad \mathrm{NC}^{-1}$

Answer 1

Answer: (A)

$L=\pi R$
$\Rightarrow R = \frac{L}{\pi } = \frac{20}{100 \pi } \, \, \text{m} = \frac{1}{5 \pi } \, \, \text{m}$
$\Rightarrow $ due to a charge arc, electric field at centre is given by
$E = \frac{2 K \lambda }{R} sin \frac{\theta }{2}$

$E_{1}=E_{2}=\frac{2 k ⋋}{R}sin \frac{90}{2} \, \, \, \left\{\right. ⋋ = \frac{Q}{\pi R / 2} \left.\right\}$

$E_{1} = E _{2} = \frac{2 \sqrt{2} \, K Q}{\pi R^{2}}$
Component along $\hat{j} \, $ gets cancelled and
$E_{n e t} = \sqrt{2} E_{1}$
$= \frac{4 K Q}{\pi R^{2}}$
$=\frac{4 \times 1\left(10^3 \epsilon_0\right)}{4 \pi \epsilon_0 \pi R^2}=\frac{4 \times 10^3 \epsilon_0}{4 \pi^2 \epsilon_0 R^2}=\frac{10^2}{R^2}=\frac{100}{\left(\frac{1}{5 \pi}\right)^2}=25 \times 10^3$
$\overset{ \rightarrow }{E}_{n e t}=25\times 10^{3}\frac{N}{C} \, \hat{i}$