Q.
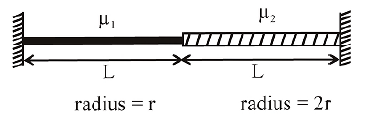
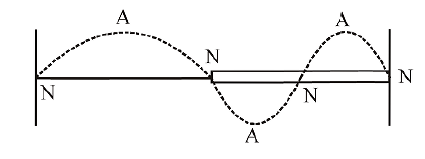
A wire of length $2L$, is made by joining two wires $A$ and $B$ of same length but different radii $r$ and $2r$ and made of the same material. It is vibrating at a frequency such that the joint of the two wires forms a node. If the number of antinodes in wire $A$ is $p$ and that in $B$ is $q$ then the ratio $p : q$ is :
Solution:
Let mass per unit length of wires are $\mu_{1}$ and $\mu_{2}$ respectively. $\because$ Materials are same, so density $\rho$ is same.
$\mu_{1}=\frac{\rho \pi r^{2} L}{L}=\mu$ and $\mu_{2}=\frac{\rho 4 \pi r^{2} L}{L}=4 \mu$
Tension in both are same $= T$, let speed of wave in wires are $V _{1}$ and $V _{2}$
$V _{1}=\sqrt{\frac{ T }{\mu}}= V ; V _{2}=\sqrt{\frac{ T }{4 \mu}}=\frac{ v }{2}$
So fundamental frequencies in both wires are
$f _{01}=\frac{ V _{1}}{2 L }=\frac{ V }{2 L } \& f _{02}=\frac{ V _{2}}{2 L }=\frac{ V }{4 L }$
Frequency at which both resonate is L.C.M of
both frequencies i.e. $\frac{ V }{2 L }$.
Hence no. of loops in wires are 1 and 2 respectively.