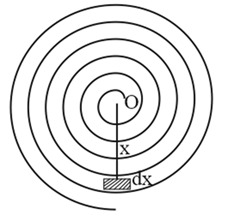
Question

A wire is tightly wound to form of a spiral of $N$ turns with the inner and outer radii equal to $a$ and $b$ respectively. When a current $I$ is established in the coil, the magnetic field at the centre is

• A. $\frac{\mu _{0} N I}{b}$
• B. $\frac{\mu _{0} N I}{a}$
• C. $\frac{\left(\mu \right)_{0} N I}{2 \left(b - a\right)}ln\left(\frac{b}{a}\right)$
• D. $\frac{\left(\mu \right)_{0} N I}{ \left(b - a\right)}ln\left(\frac{b}{a}\right)$

Answer 1

Answer: (C)

An element is assumed at distance $x$ from center whose width is $dx$ . No. of turns in width $b-a=N$
$\therefore $ No. of turns is width $dx=n=\left(\frac{N}{b - a}\right)dx$
$d B=\frac{\mu_{0} n i}{2 x}=\frac{\mu_{0} i N d x}{2(b-a)^{x}}$
$\therefore B =\frac{\mu_{0} iN }{2( b - a )} \int_{ a }^{ b } \frac{ dx }{ X }=\frac{\mu_{0} Ni }{2( b - a )} \log _{ e }\left(\frac{ b }{ a }\right)$