Q.
A wire is bent at an angle $\theta$. A rod of mass $m$ canslide along the bended
wire without friction as film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is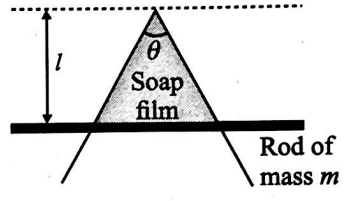
Oscillations
Solution:
