Question

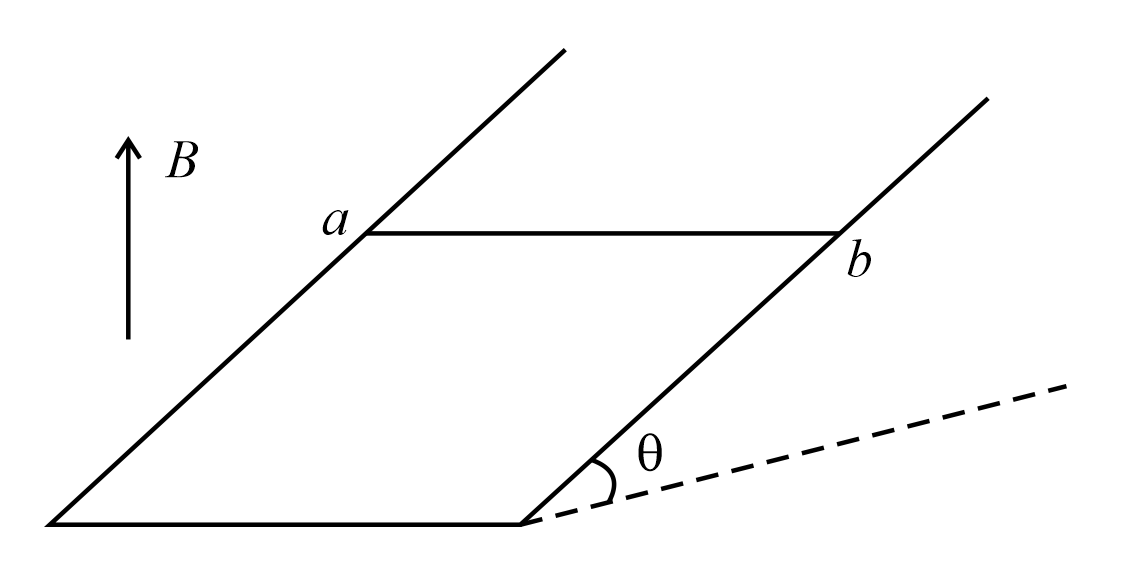
A wire ab of length $l$ , mass $m$ and resistance $R$ slides on a smooth thick pair of metallic rails joined at the bottom as shown in fig. The plane of the rails makes an angle $\theta $ with the horizontal. A vertical magnetic field $B$ exist in the region. If the wire slides on the rails at a constant speed $v$ , then the value of $B$ is -

• A. $\sqrt{\frac{m g R}{v l^{2} cos^{2} \theta }}$
• B. $\sqrt{\frac{m g R cos \theta }{v l^{2} s i n^{2} \theta }}$
• C. $\sqrt{\frac{m g R}{v^{2} l^{2} s i n^{2} \theta }}$
• D. $\sqrt{\frac{m g R sin \theta }{v l^{2} cos^{2} \theta }}$

Answer 1

Answer: (D)

The emf induced in the wire moving at a constant velocity $v$ is
$E=\left(B \cos \theta \right)lv$
So the current through the wire will be
$I=\frac{\left(B \cos \theta \right) l v}{R}$
Since the rod is moving uniformly, the net force acting on it will be zero. Balancing the forces along the direction of motion of the rod, we get
$mg \sin\theta =Il B \cos\theta $
$mg \sin\theta =\frac{v B l \cos \theta }{R}\times lB \cos\theta $
$B=\sqrt{\frac{m g R \sin \theta }{v l^{2} \cos^{2} \theta }}$