Question

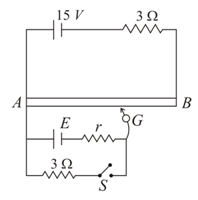
A wire $AB$ (of length $1\,m,$ area of cross section $\pi m^{2}$ ) is used in potentiometer experiment to calculate emf and internal resistance $\left(r\right)$ of battery. The emf and internal resistance of driving battery are $15\,V$ and $3\Omega$ respectively. The resistivity of wire $AB$ varies as $\rho =\rho _{0}x,$ where $x$ is distance from $A$ in meters and $\rho _{0}=24\pi \Omega.$ The distance of null point from $A$ is obtained at $\sqrt{\frac{2}{3}}m$ when switch $'S'$ is open. Find the value of $E.$

Answer 1

$R_{A B}= \int\limits _{0}^{1}\frac{\rho _{0} X d X}{A}$
$= \int\limits _{0}^{1}\frac{24 \pi X d X}{A}=12\Omega$
$R_{A G}= \int\limits _{0}^{\sqrt{\frac{2}{3}}}\frac{24 \pi X d X}{\pi }=\frac{24}{2}\left[X^{2}\right]_{0}^{\sqrt{\frac{2}{3}}}$
$=12\times \frac{2}{3}\,\Omega$
$i_{in }$ wire $=\frac{15}{3 + 12}=1\,A$
$V_{A G}=1\times 8=8\,V$