Question

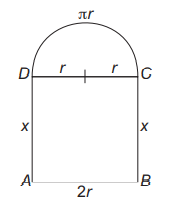
A window is in the form of a rectangle surmounted by a semi-circular opening. The total perimeter of the window is $10 m$.
Statement I One of the dimension of the window to admit maximum light through the whole opening is $\frac{20}{\pi+4} m$
Statement II One of the dimension of the window to admit maximum light through the whole opening is $\frac{10}{\pi+4} m$.

• A. Only statement I is true
• B. Only statement II is true
• C. Both the statements are true
• D. None of the above

Answer 1

Answer: (C)

Let radius of semi-circle $=r$
$\therefore$ One side of rectangle $=2 r$. Let other side $=x$
$\because P=$ Perimeter $=10$ (given)
$\Rightarrow 2 x+2 r+\frac{1}{2}(2 \pi r)=10$
$\Rightarrow 2 x=10-r(\pi+2) ......$(i)
Let $A$ be area of the window, then
$ A=$ Area of semi-circle $+$ Area of rectangle $=\frac{1}{2} \pi r^2+2 r x $
$ \Rightarrow A=\frac{1}{2}\left(\pi r^2\right)+r[10-r(\pi+2)] $ [using Eq. (i)]
$=\frac{1}{2}\left(\pi r^2\right)+10 r-r^2 \pi-2 r^2$
$=10 r-\frac{\pi r^2}{2}-2 r^2$

On differentiating twice w.r.t. $r$, we get
$\frac{d A}{d r}=10-\pi r-4 r .....$(ii)
and $ \frac{d^2 A}{d r^2}=-\pi-4 .....$(iii)
For maxima or minima, put $\frac{d A}{d r}=0$
$\Rightarrow 10-\pi r-4 r =0$
$\Rightarrow 10 =(4+\pi) r $
$\Rightarrow r =\frac{10}{4+\pi}$
On putting $r=\frac{10}{4+\pi}$ in Eq. (iii), we get $\frac{d^2 A}{d r^2}<0$
Thus, $A$ has local maximum when
$r =\frac{10}{4+\pi}......$(iv)
$\therefore $ Radius of semi-circle $ =\frac{10}{4+\pi}$
and one side of rectangle $=2 r=\frac{2 \times 10}{4+\pi}=\frac{20}{4+\pi}$
and other side of rectangle i.e., $x$ from Eq. (i) is given by
$x =\frac{1}{2}[10-r(\pi+2)] $
$ =\frac{1}{2}\left[10-\left(\frac{10}{\pi+4}\right)(\pi+2)\right] $[from Eq. (iv)]
$=\frac{10 \pi+40-10 \pi-20}{2(\pi+4)}$
$ =\frac{20}{2(\pi+4)} $
$ =\frac{10}{\pi+4}$
Light is maximum when area is maximum.
So, dimensions of the window are length $=2 r=\frac{20}{\pi+4}$, breadth $=x=\frac{10}{\pi+4}$.
So, both the statements are true.