Q.
A wheel of radius $R=10\, cm$ and moment of inertia $I=0.05 \, kg\, m ^{2}$ is rotating about a fixed horizontal axis $O$ with angular velocity $\omega_{0}=10 \, rad / \sec$. A uniform rigid rod of mass $m=3\, kg$ and length $l=50\, cm$ is hinged at one end $A$ such that it can rotate about end $A$ in a vertical plane. End $B$ of the rod is tied with a thread as shown in figure such that the rod is horizontal and is just in contact with the surface of rotating wheel. Horizontal distance between axis of rotation $O$ of cylinder and $A$ is equal to $a$ $=30\, cm$. The wheel stops rotating after one second after the thread has burnt. If the coefficient of friction $\mu$ between the rod and the surface of the wheel is equal to $\frac{x}{5}$. Then the value of $x$ is _____$.\left(g=10\,ms ^{-2}\right)$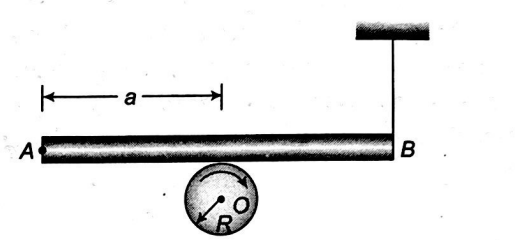
System of Particles and Rotational Motion
Solution:
