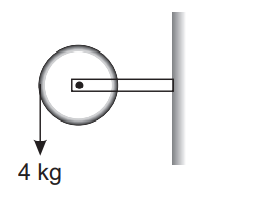
Question

A wheel of radius $0.4 \,m$ can rotate freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of $4 \,kg$ is hung. An angular acceleration of $8\, rad - s ^{-2}$ is produced in it due to the torque. Then, moment of inertia of the wheel is $\left(g=10 \,ms ^{-2}\right.$ )

• A. $2 \,kg - m ^{2}$
• B. $1\,kg - m ^{2}$
• C. $4 \,kg - m ^{2}$
• D. $8 \,kg - m ^{2}$

Answer 1

Answer: (A)

Given, $r=0.4\, m$,
$\alpha=8 \,rad\, s ^{-1}$
$m=4\, kg , I=?$
Torque, $\tau=I \alpha$
$m g r=I \cdot \alpha$
or $4 \times 10 \times 0.4=I \times 8$
$\Rightarrow I=\frac{16}{8}=2 \,kg - m ^{2}$
or $I=2 \,kg - m ^{2}$