Q.
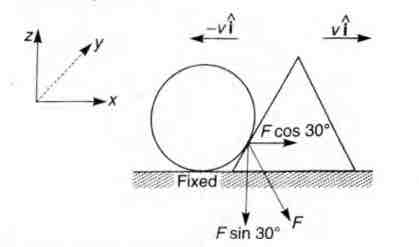
A wedge of mass m and triangular cross-section
(AB = BC = CA = 2R)is moving with a constant velocity
(-v $\widehat{i}$) towards a sphere of radius R fixed on a smooth
horizontal table as shown in the figure.
The wedge makes an elastic collision with the fixed sphere
and returns along the same path without any rotation. Neglect
all friction and suppose that the wedge remains in contact
with the sphere for a very short time $\Delta$t during which the
sphere exerts a constant force F on the wedge.
(a) Find the force F and also the normal force N exerted by
the table on the wedge during the time $\Delta$t.
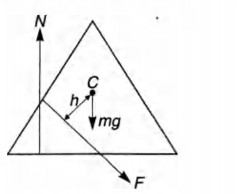
(b) Let h denote the perpendicular distance between the
centre of mass of the wedge and the line of action of F.
Find the magnitude of the torque due to the normal force
N about the centre of the wedge during the interval $\Delta$t.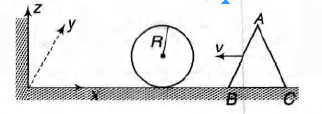
IIT JEEIIT JEE 1978Oscillations
Solution:
(i) Since, the collision is elastic, the wedge will return
with velocity v $\widehat{i}$.
Now, linear impulse in .v-direction
= change in momentum in .r-direction.
$\therefore \, \, (F cos 30 ^\circ ) \Delta t = mv - (- mv) = 2mv $
$\therefore \, \, \, F = \frac{ 2mv }{\Delta t cos 30 ^\circ } = \frac{ 4mv }{\sqrt 3 \Delta t } \rightarrow F =\frac{ 4mv }{\sqrt 3 \Delta t } $
$ \therefore \, \, \, F= ( Fcos 30 ^\circ ) \widehat{i} - ( Fsin 30 ^\circ ) \widehat{k}$
or $ \, \, \, \, \, F = \bigg( \frac{ 2mv}{ \Delta t } \bigg)\widehat{i} - \bigg( \frac{ 2mv}{ \sqrt 3 \Delta t } \bigg)\widehat{k}$
(ii) Taking the equilibrium of wedge in vertical
z-direction during collision
.(b) For rotational equilibrium of wedge [about (CM)]
anticlockwise torque of F = clockwise torque due to N
$\therefore $ Magnitude of torque of N about CM = magnitude of
torque of F about CM
$ \, \, \, \, \, \, \, \, \, = F.h $
$ | {\tau}_N | = \bigg( \frac{ 4 mv }{ \sqrt 3 \Delta t }\bigg) h $