Q.
A wedge, as shown in the figure, has a rough curved surface with coefficient of kinetic friction $\frac{1}{\sqrt{3}}$ and whose shape can be given by equation $y=x^{2}$, where the horizontal direction is $x$-axis the vertical direction is $y$-axis, the end of surface is $O$ as origin and $x$ and $y$ are measured in metre. A small block is released from a certain point on the surface. The maximum height of the point from where the block should be released so that it does not slip is $\frac{m}{n}$. metre. Find $m n$.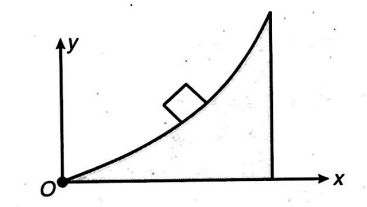
Laws of Motion
Solution: