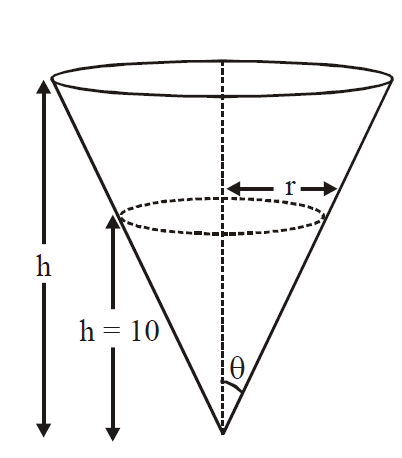
Q. A water tank has the shape of an inverted right circular cone, whose semi-vertical angle is $\tan^{-1} \left(\frac{1}{2}\right)$ . Water is poured into it at a constant rage of $5$ cubic meter per minute. The the rate (in m/min.), at which the level of water is rising at the instant when the depth of water in the tank is $10\,m$; is :-
Solution:
$\tan\theta = \frac{1}{2} = \frac{r}{h} $
$ r = \frac{h}{2} $
$V = \frac{1}{3} \pi r^{2}h $
$ V = \frac{1}{3} \pi. \frac{h^{3}}{4} $
$\frac{dV}{dt} = \frac{\pi}{12} \left(3h\right)^{2} \left(\frac{dh}{dt}\right) $
$ 5 = \frac{\pi}{4} .\left(100\right) \frac{dh}{dt} \Rightarrow \frac{dh}{dt} = \frac{1}{5\pi} $