Q.
A water cooler of storage capacity $120$ liters can cool water at a constant rate of $P$ watts. In a closed circular system (as shown schematically in the figure), the water from the cooler is used to cool an external device that generates constantly $3 kW$ of heat (thermal load). The temperature of water fed into the device cannot exceed $30^{\circ} C$ and the entire stored $120$ litres of water is initially cooled to $10^{\circ} C$. The entire system is thermally insulated. The minimum value of $P$ (in watts) for which the device can be operated for $3$ hours is
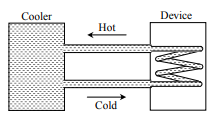
(Specific heat of water is $4.2\, kJ kg ^{-1} K ^{-1}$ and the density of water is $1000\, kg m ^{-3}$ )
JEE AdvancedJEE Advanced 2016
Solution: