Question

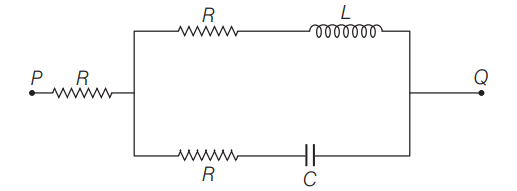
A voltage $V_{PQ} = V_0 \, \cos \, \omega t$ (where $V_0$ is a real amplitude) is applied between the points P and Q in the network shown in the figure. The values of capacitance and inductance are $C = \frac{1}{\omega R \sqrt{3}}$ and $L = \frac{R \sqrt{3}}{\omega}$
Then, the total impedance between P and Q is

• A. 1.5 R
• B. 2R
• C. 3R
• D. 4R
• E. 2.5 R

Answer 1

Answer: (C)

$\because$ Given that, $C=\frac{1}{\omega R \sqrt{3}}, L=\frac{R \sqrt{3}}{\omega}$

In the above figure,
$Z_{1}=R +j \omega L=R+ j \omega\left(\frac{R \sqrt{3}}{\omega}\right)=R +j R \sqrt{3}$
$Z_{2}=R-j \frac{1}{\omega c}=R-j \frac{1}{\omega\left(\frac{1}{\omega R \sqrt{3}}\right)}=R-j R \sqrt{3}$
$\because$ Impedance $Z_{1}$ and $Z_{2}$ are in parallel,
So, $Z_{\text {eq }}= \frac{Z_{1} Z_{2}}{Z_{1}+Z_{2}}$
$=\frac{(R +j R \sqrt{3})(R-j R \sqrt{3})}{R +j R \sqrt{3}+R-j R \sqrt{3}}$
$=\frac{R^{2}+R^{2}(\sqrt{3})^{2}}{2 R}$
$\left(\because(a-b)(a +b)=a^{2}-b^{2}\right)$
$Z_{ eq }=\frac{4 R^{2}}{2 R}=2 R$
So, total impedance between $P$ and $Q$ is
$Z_{P Q}=R+Z_{ eq }$
$Z_{P Q}=R+2 R=3 R$