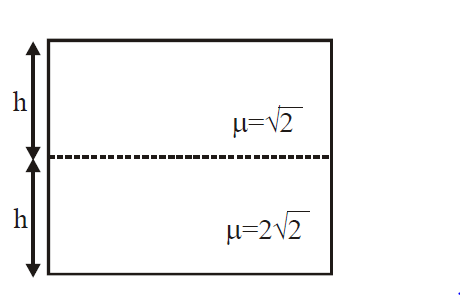
Q. A vessel of depth $2\,h$ is half filled with a liquid of refractive index $2\sqrt{2}$ and the upper half with another liquid of refractive index $\sqrt{2}$ The liquids are immiscible. The apparent depth of the inner surface of the bottom of vessel will be :
Solution:
For near normal incidence,
$h_{app}=\frac{h_{actual}}{\left(\frac{\mu_{in}}{\mu_{ref.}}\right)}$
$\therefore h_{apparent}=\frac{\frac{h}{\left(\frac{2\sqrt{2}}{\sqrt{2}}\right)}+h}{\frac{\sqrt{2}}{1}}=\frac{3h}{2\sqrt{2}}=\frac{3}{4}h\sqrt{2}$