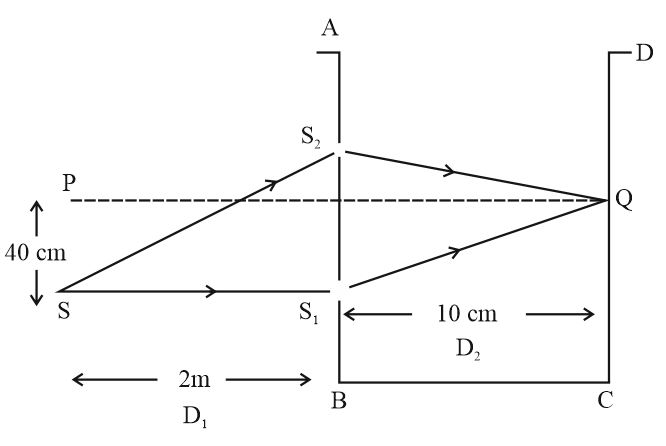
Question

A vessel $\text{ABCD}$ of $\text{10 cm}$ width has two small slits $\text{S}_{1}$ and $\text{S}_{2}$ sealed with identical glass plates of equal thickness. The distance between the slits is $\text{0} \text{.8 mm}$ . $\text{POQ}$ is the line perpendicular to the plane $\text{AB}$ and passing through $\text{O}$ , the



middle point of $\text{S}_{1}$ and $\text{S}_{2}$ , A monochromatic light source is kept at $\text{S}$ , $\text{40 cm}$ cm below $\text{P}$ and $\text{2 m}$ from the vessel, to illuminate the slits as shown in the figure alongside. After a liquid is poured into the vessel and filled upto $\text{OQ,}$ it was found that the central bright fringe is now located at $\text{Q}$ . Calculate the refractive index of that liquid.

• A. $\text{1.0016}$
• B. $\text{2} \text{.0032}$
• C. $\text{1} \text{.0010}$
• D. $\text{1} \text{.0026}$

Answer 1

Answer: (A)

Given, $d = 0.8 \, \text{mm}$
$\text{y}_{1} = 40 \text{ cm, D}_{1} = 2 \, \text{m}$

Thickness of liquid having refractive index $\mu $ is given by $t = D_{2} = 10 \, \text{cm}$
Initial path difference
$\text{Δx}_{\text{1}} , \, = \text{ SS}_{1} - \text{SS}_{2} = \frac{\text{y}_{\text{1}} \text{d}}{\text{D}_{\text{1}}}$
For central maxima of $Q$ , optical path difference introduced by liquid of refractive index $\mu $ should be compensate for initial path difference
i.e. $\left(\mu - 1\right) t = \Delta x_{1}$
$\mu = 1 + \frac{\Delta \text{x}_{1}}{\text{t}} = 1 + \frac{\text{y}_{1} \text{d}}{\text{t D}_{1}}$
$= 1 + \frac{0 \text{.} 4 \text{m} \times 0 \text{.} 8 \text{mm}}{0 \text{.} 1 \text{m} \times 2 \text{m}}$
$= 1 + 2 \times 0 \text{.} 8 \times 1 0^{- 3}$
$= 1 + 1 \text{.} 6 \times 1 0^{- 3}$
$= 1 \text{.} 0 0 1 6$