Question

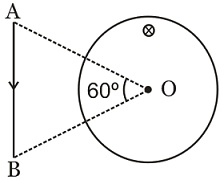
A very long cylindrical wire is carrying a current $I_{o}$ distributed uniformly over its cross-section area. $O$ is the centre of the cross-section of the wire and the direction of current in into the plane of the figure. The value of $\displaystyle \int _{A}^{B}\overset{ \rightarrow }{B}.\overset{ \rightarrow }{dI}$ along the path $AB$ (from $A$ to $B$ ) is

• A. $\mu _{0}I_{0}$
• B. $-\frac{\mu _{0} I_{0}}{6}$
• C. $\frac{\mu _{0} I_{0}}{6}$
• D. $\frac{\mu _{0} I_{0}}{3}$

Answer 1

Answer: (B)

According to Ampere's circuital law
$\oint\overset{ \rightarrow }{B}.\overset{ \rightarrow }{dl}=\mu _{0}I_{net}$
For the closed path $OAB$
$\oint\overset{ \rightarrow }{B}.\overset{ \rightarrow }{dl}=\displaystyle \int _{O}^{A}\overset{ \rightarrow }{B}.\overset{ \rightarrow }{dl}+\displaystyle \int _{A}^{B}\overset{ \rightarrow }{B}.\overset{ \rightarrow }{dl}+ \, \displaystyle \int _{B}^{O}\overset{ \rightarrow }{B}.\overset{ \rightarrow }{dl}=\left(\mu \right)_{0}\left(- \frac{I_{0}}{6}\right)$
Since the magnetic field is perpendicular to the paths $OA$ and $BO$
$\displaystyle \int _{A}^{B}\overset{ \rightarrow }{B}.\overset{ \rightarrow }{dl}=-\frac{\mu _{0} I_{0}}{6}$